Linking ab initio energetics with phase diagram predictions

Soumya Sridar is pursuing her Integrated PhD (M Tech+PhD) with Prof K C Hari Kumar and Prof N V Ravi Kumar in Department of Metallurgical and Materials Engineering, IIT Madras. She is currently working in the field of developing phase diagrams of transition metal containing nitride systems using Calphad approach coupled with ab initio methods. email: soumya_sridar@yahoo.co.in

Thermodynamics deals with the equilibrium state of a system, which is a necessary foundation for phase transformations and processes. One of the important manifestations of thermodynamics is phase diagrams. Phase diagrams are useful graphical representations of the phase changes in a material. They serve as a road map for materials design and process optimization since it is the starting point in the manipulation of processing variables to achieve the desired microstructure. This article gives a bird’s eye view about how phase diagrams can be determined using computational techniques. For further understanding, the readers can refer to the books mentioned in the Reference section for each technique discussed in this article. The Calphad method: Engineering materials are multicomponent systems and application of thermodynamics for these systems are rather limited. It is difficult to obtain phase diagrams for multicomponent systems with experiments alone. Calculation of Phase Diagrams (Calphad) is a reliable tool to generate multicomponent phase diagrams which has been used for over 30 years. The Calphad method was pioneered by Kaufman and Bernstein and further developed by Hillert and others. It is based on the simple thermodynamic concept that a system with a given composition, pressure and temperature attains the state of lowest Gibbs energy i.e., equilibrium under these conditions. If the Gibbs energy is known for the individual phases in a system, it is possible to calculate the equilibrium state using an energy minimization procedure. The expression for Gibbs energy function which is widely used for Calphad modelling at 1 atm pressure is

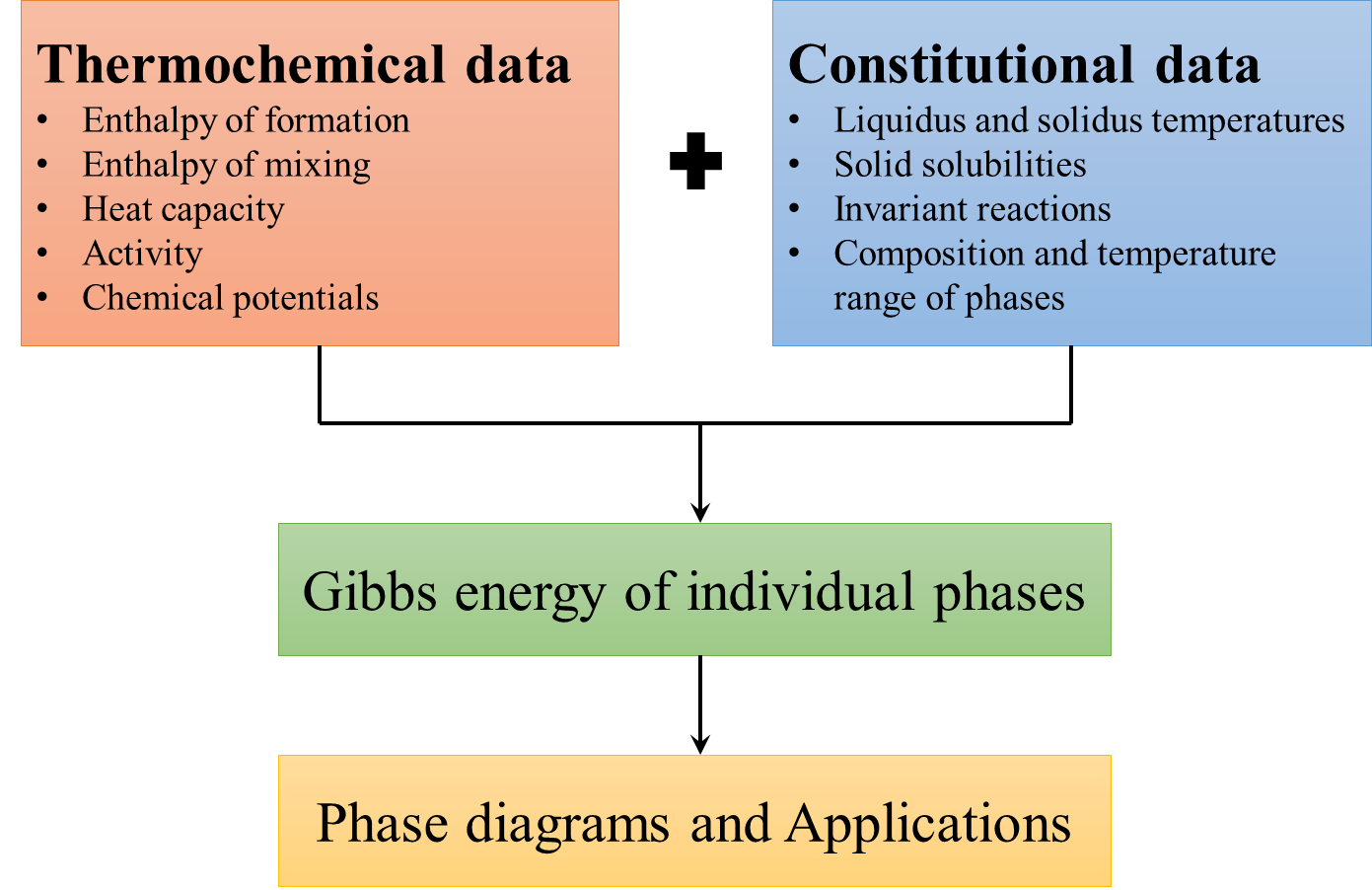
The parameters such as a, b, c, d, e and f needs to be determined for each phase in a system using statistical techniques with relevant data as input. The method involves minimizing reduced sum of squares of errors in an iterative manner, starting with guess values for all optimizing variables. Optimization is initialized by providing guess values for the parameters. The start values are refined iteratively minimizing the sum of the squares of deviation between input data and the corresponding model calculated values. This whole process is known as thermodynamic optimization or assessment. The optimized Gibbs energy parameters thus obtained, are eventually used for calculating phase diagrams and thermochemical properties at any desired temperature and composition regime in which the functions are valid. Commercial softwares such as Thermo-Calc and Pandat as well as open source softwares like Open Calphad can be utilized for this purpose. The input data required are summarized in the schematic for thermodynamic optimization as shown in Figure 1. Integrating ab initio with Calphad: Thermochemical data is usually for individual phases and scarcer than constitutional data which usually involves more than one phase and is relatively easier to obtain experimentally. Ab initio calculations thus complement experiments ideally by providing much needed thermochemical data of individual phases. These inputs are particularly valuable for compositions or phases that cannot be measured experimentally, because the phase is metastable or its formation is too slow or due to other experimental difficulties such as oxidation, evaporation, exothermic reactions and so on. Ab initio calculations, based on density functional theory (DFT) requires only knowledge of the atomic species and crystal structure, and yield quantities related to the electronic structure and total energy of a given structure. For thermodynamic properties of alloys, one currently needs to estimate different contributions such as, static energy or the 0 K total energy thermodynamic properties at finite temperatures from lattice thermal vibrations

Total energy at 0 K using DFT: A solid can be thought of as a collection of interacting, positively charged nuclei and negatively charged electrons and can theoretically be treated by solving the many-body Schrodinger equation involving both the nuclei and the electrons.

where is the nuclei co-ordinate, is the electron co-ordinate, is the Hamiltonian operator, E is the eigenvalue or the energy and is the eigen function or the many-body wave function of the Hamiltonian. The exact Hamiltonian for a many-body system is given by where M is the mass of the nuclei and Z is the valence charge of the nuclei. It is extremely difficult to solve the equation due to its many-body nature. Several levels of approximations have been introduced to obtain numerical solutions to the Schrodinger equation. The atoms are kept static in their lattice positions in these crystal in these calculations using DFT. There are commercial (VASP, CASTEP and Wien2K) as well as open source (Quantum espresso, SIESTA and ABINIT) codes to perform these calculations. The ground state total energy for a solid obtained from these calculations can be used for estimating the enthalpy of formation at 0 K. When there are no phase transitions for the pure elements and compounds between 0 K and room temperature, the enthalpy of formation of a stable or metastable compound at 298 K, can be approximated by the following equation.

where is the total energy at 0 K from DFT calculations. The calculated enthalpies of formation can be used as an input for thermodynamic modelling, which significantly enhances its robustness. Also, the accuracy is often found to be similar to good calorimetric data from experiments. Finite temperature thermodynamic properties using ab initio phonons: At finite temperatures, atoms tend to fluctuate around their equilibrium lattice positions, resulting in lattice vibrations which can be represented by elastic waves made of phonons. Their energy is quantized which is proportional to the angular frequency of each elastic mode. Thermodynamic relations can be derived on the basis of statistical mechanics from the phonon dispersion relation and summarized in terms of the phonon density of states (DOS). In the phonon approach, ab initio calculations can be performed with a harmonic approximation to obtain the full phonon spectra for a given atomic configuration. The ground state structure from DFT serves as input for these phonon calculations. The restoring force constants , on atom i due to the displacement of atom j are computed from the second derivatives of the energy change with respect to the displacements. The main approach for determining the force constants is the supercell method, also known as “frozen” phonon method. In this method, the atoms are displaced slightly from their equilibrium positions, and the reaction forces are calculated. The displacements can be considered as snapshots of crystal during vibration. The displacements and reaction forces are then used to evaluate the force constants. Since, supercells are involved, these calculations are computationally very expensive. One simple approach beyond the harmonic approximation to account for anharmonicity is the so called quasiharmonic approximation. This accounts for thermal expansion and its effect on the vibrational properties. In this approximation, the phonon DOS, is made volume dependent by calculating the phonon DOS for several volumes within the harmonic approximation. The common codes which are used for performing the phonon calculations are PHONON, Phonopy, PHON and fitfc module of Alloy Theoretic Automated Toolkit (ATAT). The quantities that can be estimated as function of temperature using these calculations are heat capacity at constant pressure (Cp), Gibbs energy (G), coefficient of thermal expansion (α) and bulk modulus (B). The Cp(T) and G(T) values are useful inputs which can be used for thermodynamic modelling using Calphad method. An example: Si-N system: Si-N system is a very simple and the phases present in this system are gas, liquid, αSi3N4, βSi3N4 and Si. Both the α- and β- polymorphs of Si3N4 possess hexagonal structure with different space groups. In order to obtain the Gibbs energy descriptions for this system ab initio calculations were used to estimate the thermochemical data. DFT calculations were performed for α- and β- polymorphs of Si3N4 and the values obtained are summarized in Table 1. It can be seen that the difference between the calculated and experimental enthalpy of formation is less than 5%, which is within the error limits of a calorimetric measurement. Since, there were no measurement of thermochemical quantities in literature for both the polymorphs above room temperature, quasiharmonic approximation was used for estimating the finite temperature thermodynamic properties for α- and β- polymorphs of Si3N4. Table 1: Comparison between calculated and experimental enthalpies of formation for Si3N4

The Cp values obtained from these calculations are shown in Figure 2. Amongst the two polymorphs of Si3N4, there is ambiguity in the thermodynamically stable state. From the phonon calculations, the difference in Gibbs energies of α- and β- polymorphs of Si3N4 shows that βSi3N4 is the thermodynamically stable state. With all these inputs from ab initio calculations and constitutional data from literature, thermodynamic modelling was carried out to obtain the Gibbs energy parameters for different individual phases in Si-N system. The calculated phase diagram with these descriptions is shown in Figure 3.

References: Calphad method:

1. CALPHAD: Calculation of Phase Diagrams: A Comprehensive Guide by N Saunders and A P Miodownik
2. Computational Thermodynamics: The Calphad Method by H L Lukas, Suzana G Fries and Bo Sundman
3. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis by Mats Hillert Elementary Quantum Mechanics:
4. A chemist’s guide to density functional theory by Wolfram Koch and Max C. Holthausen
5. Principles of quantum mechanics by R Shankar Density Functional Theory:
6. Density Functional Theory: A Practical Introduction by David S Scholl and Janice A Steckel
7. Materials modelling using Density Functional Theory: Properties and Prediction by Feliciano Giustino Phonons and Lattice dynamics:
8. Introduction to lattice dynamics by Martin T Dove
9. Electrons and Phonons by J M Ziman